MODELING LEAF OPTICAL PROPERTIES
Stéphane Jacquemoud1 and Susan L. Ustin2
1Géophysique Spatiale et Planétaire
Institut de Physique du Globe de Paris - Université Paris Diderot
75013 Paris, France
jacquemoud@ipgp.jussieu.fr
2Department of Land, Air and Water Resources
University of California, Davis, CA 95616, U.S.A.
slustin@ucdavis.edu
Introduction
Higher plants have proliferated a wide range of internal leaf structures, and yet they demonstrate ecological convergences in similar ecosystems, which are widely interpreted to indicate evolutionary constraints on optimized leaf properties. Plant leaves are the primary photosynthesizing organs, significantly affecting important planetary biogeochemical cycles. The mechanisms of how leaf chemistry, structure and orientation interacts with the light environment, however, remains incompletely understood. Leaf optical properties, have been extensively studied for 150 years, although primarily for Angiosperms. It is well established that the reflectance and transmission spectrum of leaves is a function of both the concentration of light absorbing compounds (chlorophylls, carotenoids, water, cellulose, lignin, starch, proteins, etc.), and the internal scattering of light that is not absorbed or absorbed less efficiently. Quantitative relationships between optical characteristics and plant biochemical properties (which themselves depend on many environmental and species factors), have been established empirically, such as response to leaf aging or environmental stresses, which are well known to reduce chlorophyll content, which in turn, increases both the reflectance and transmittance in the visible spectrum. More recently, radiative transfer models of leaf biophysical processes have been used to directly estimate biochemical composition and structural characteristics. An extensive review of the literature, and available optical models is available ONLINE.
1. Optical Observations of Plant Leaves
When a leaf intercepts a light beam, it can be partly reflected, transmitted or absorbed. The sum of the reflectance R, transmittance T, and absorptance A, equals one:
(1)
R + T + A = 1
The reflectance can be split into two terms: a fraction, Rs , is reflected at the leaf surface and a fraction, Rd , is caused by multiple scattering within the leaf tissues. The subscripts s and d stand for surface (or for specular since most leaves display such an optical behavior), and diffuse, respectively. In the following discussion, only the diffuse reflectance and transmittance are considered in models.
The domain of optical observations extends from 400 nm in the visible region of the electromagnetic spectrum to 2500 nm in the shortwave infrared region (Figure 1). The strong absorption of light by photosynthetic pigments dominates green leaf properties in the visible spectrum (VIS, 400 nm - 700 nm). Leaf chlorosis causes an increase in visible reflectance and transmission. The near-infrared plateau (NIR, 700 nm - 1100 nm), is a region where biochemical absorptions are limited to the compounds typically found in dry leaves, primarily cellulose, lignin and other structural carbohydrates. However, foliar reflection in this region is also affected by multiple scattering of photons within the leaf, related to the internal structure, fraction of air spaces, and air-water interfaces that refract light within leaves. The reflectance and transmittance in the middle-infrared also termed the shortwave-infrared (SWIR, 1100 nm - 2500 nm) is also a region of strong absorption, primarily by water in green leaves. The primary and secondary absorptions of water in leaf reflectance are greatest in spectral bands centered at 1450, 1940, and 2500 nm, with important secondary absorptions at 980 nm, and 1240 nm (Carter, 1991).
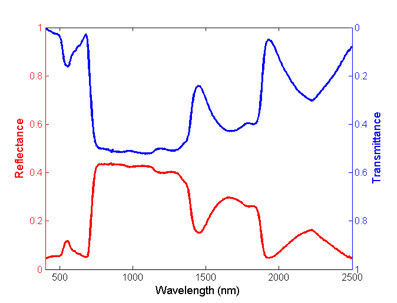
Figure 1. Reflectance (red) and transmittance (blue) spectra of a fresh Carolina poplar (Populus canadensis) leaf.
In dry leaves, reflectance and transmission are influenced by dry carbon compounds like cellulose and lignin, nitrogen, sugars, and other plant compounds (Figure 2). For example, nitrogen (N-H bonds) have a first harmonic overtone at 1510 nm and a series of combination bands at 1980, 2060, and 2180 nm (Wessman, 1990).
Figure 2. Reflectance (red) and transmittance (blue) spectra of a dry Carolina poplar (Populus canadensis) leaf.
2. Different Approches for Leaf Diffuse Optical Properties
As pointed out by Wang et al. (2005), leaf optical properties are particularly difficult to simulate due to their intricate underlying structure and their complex and subtle interaction with light. The propagation of light through plant leaves is governed primarily by absorption and scattering interactions. While experimental measurements of leaf optical properties were progressing, deterministic approaches based on diverse representations of light interactions with plant leaves were also developed. These models are distinguished by the underlying physics and by the complexity of the leaf. The simplest ones consider the blade as a single scattering and absorbing layer. In the most complicated ones, all the cells are described in detail by their shape, size, position, and biochemical content. At a minimum, physically realistic models require information about the refractive index and the specific absorption coefficients of leaf constituents (Figure 3). The absorption spectrum of chlorophyll expands over the entire visible region from 400 nm to 750 nm, with a minimum at 550 nm. The absorption spectrum of water starts at wavelengths longer than 950 nm, with three main absorption peaks as cited above. Lastly, the absorption spectrum of leaf dry matter is minimal (~ <0.1, see Figure 1) in the visible and near-infrared, and stronger at wavelengths longer than 1200 nm. None of these compounds absorbs much energy in the region between 750 nm and 1250 nm, which explains why leaf reflectance and transmittance are high in this region.
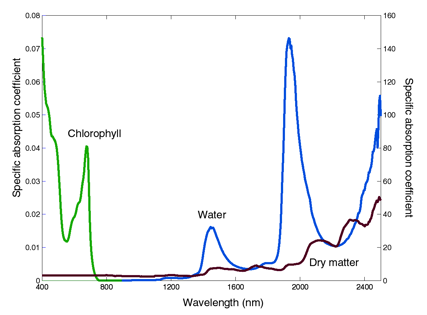
Figure 3. Specific absorption coefficient of chlorophyll a+b (cm2 µg-1) on the left axis, of water (cm-1) and dry matter
(cm2 g-1) on the right axis (after Jacquemoud et al., 2000).
Whatever the approach, these models have improved our understanding of the interactions of light with plant leaves. Baranoski and Rokne (2004) and Ustin et al. (2004) extensively reviewed computer-based leaf models which, from the late sixties to the present, have improved our understanding of the interaction of light with plant leaves. They can be categorized into different classes, arranged in order of increasing complexity:
a) Plate Models
The plate model developed by Allen et al. (1969) considers a compact plant leaf as a semi-transparent plate with plane parallel surfaces and initially assumes that the incident light is partially isotropic. That requirement is equivalent to the assumption that the surfaces are rough. Figure 4 illustrates incident light interacting with a compact plant leaf: it is partly reflected, partly transmitted and partly absorbed.
Figure 4. Schematic representation of a monocot leaf (left) and multiple reflections produced by a single plate (right).
The expression for the total reflectance of the plate, R, can be derived by summing the amplitudes of successive reflections and refractions. Such derivation was first carried out in 1833 by Sir George Biddell Airy. Consider a beam incident on the plate: it is partially reflected and partially transmitted at the first interface. The transmitted part is subsequently reflected back and forth between the two interfaces as shown. We obtain:
(2)
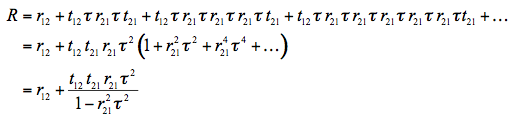
where r12 and t12 are the average reflectivity and transmissivity, respectively, from medium 1 into medium 2 (same argument for r21 and t21), and
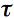is the fraction of light transmitted through the medium. The total transmittance of the plate, T, is also determined by summing the components of transmissions to infinity:
(3)
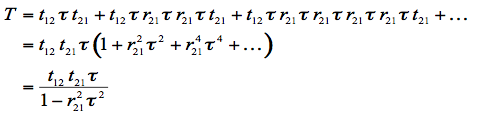
r12 is calculated from Fresnel's equations for an incidence angle θ, and a refractive index of the medium n. t12 is easily deduced via the relation r12 = 1 - t12. Remembering that t21 = t12/n2, and that r21 = 1 - t21 avoids unnecessary calculations.
is related to the absorption coefficient of the plate, k, through Beer's law. In consequence, the reflectance and transmittance of the plate only depend its index of refraction n, and its absorption coefficient k. This model was successful in reproducing the reflectance spectrum of a compact corn (Zea mays L.) leaf characterized by few air-cell wall interfaces. However, plant leaves are not compact but present a wide range of anatomical structures which depend on the species. Since plant leaves cannot be described as a unique compact layer, the plate model detailed above is not suited to simulating leaf optical properties.
Allen et al. (1970) followed by Breece and Holmes (1971) rapidly extended the plate model to non-compact leaves by introducing the generalized plate model which simply consists of stacking elementary plates. This new model accounts for the development of intercellular spaces in the leaf mesophyll. The leaf is conceptually subdivided into N uniform compact plates separated by N - 1 air spaces. Such a system has been solved for reflectance and transmittance many years ago by the Irish mathematician Stokes (1862) who actually contemplates a set of
N = m + n plates, and obtains the reflectance R(m + n) and the transmittance T(m + n) of this set in terms of the reflectances and transmittances of the two subsets consisting of m and n plates (Figure 5). The radiation flux which strikes the m plates from above is partially reflected and partially transmitted. The fraction T(m) falls on the n plates, the fraction T(m)R(n) is reflected, and the fraction T(m)T(n) transmitted. The fraction T(m)R(n) falls from beneath on the m plates, the new fraction T(m)R(n)T(m) being transmitted, and the fraction T(m)R(n)R(m) reflected, etc.
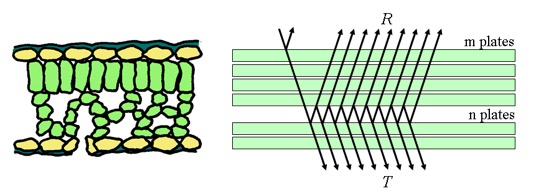
Figure 5. Schematic representation of a dicotyledon leaf (left) and multiple reflections produced by a set of N = m + n plates (right).
By summing all the reflected and transmitted fractions, we obtain two geometrical series:
(4)
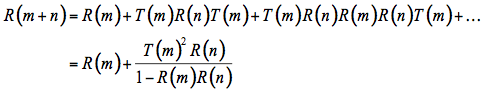
and
(5)
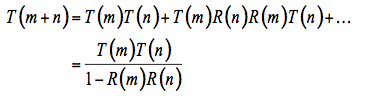
There are different ways to solve this system of recursive series (e.g., Stokes, 1962; Olf, 1988):
(6)
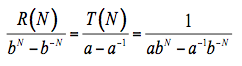
where the terms a and b depend on the reflectance and transmittance of one layer, and:
(7-9)
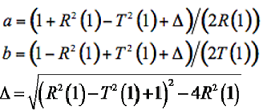
This discrete approach gave rise to an abundant literature (e.g., Benford, 1923; Gronwall, 1926; Benford, 1946; Tuckerman, 1947; Olf, 1988; Dahm and Dahm, 1999). It can be extended to a continuous approach where needs not be an integer. Now in widespread use in the remote sensing community, the PROSPECT model (Leaf Optical Properties Spectra) was designed this way (Jacquemoud and Baret, 1990). It was among the first radiative transfer codes to accurately simulate the hemispherical reflectance and transmittance of various plant leaves (monocots, dicots or senescent leaves) over the solar spectrum from 400 nm to 2500 nm. Originally the model used three input parameters: the structure parameter N (number of compact layers specifying the average number of air/cell walls interfaces within the mesophyll), the chlorophyll a+b content Cab (µg.cm-2), and the equivalent water thickness Cw (g.cm-2 or cm). Motivated by the existence of specific absorption bands in the shortwave-infrared for chemical bonds in cellulose and lignin (~carbon) or proteins (~nitrogen), that are potentially measurable by remote sensing, scientists introduced them into the model (Fourty et al. 1996; Jacquemoud et al. 1996; Fourty and Baret 1998). A limit to the resolution of biochemical constituents arose in the inversion of the model when it was discovered that protein content could not be retrieved in fresh leaves because of the strong water absorption features and in dry leaves, because cellulose and lignin were not consistently identified and quantified as separate constituents. As a consequence, the model was simplified to the point that it now considers the dry matter content
Cm (g.cm-2) as a whole instead of treating individual leaf biochemical constituents (Baret and Fourty 1997; Jacquemoud et al. 2000). The four input parameters of the PROSPECT model were: the leaf structure parameter, the chlorophyll a+b concentration, the equivalent water thickness, and the dry matter content. Ceccato et al. (2001) and Bacour et al. (2002) have quantified the contribution of each of these input biochemical parameters to the PROSPECT model outputs, as well as their interactions (Figure 6), demonstrating that most foliar absorptions are accounted for in the current model.
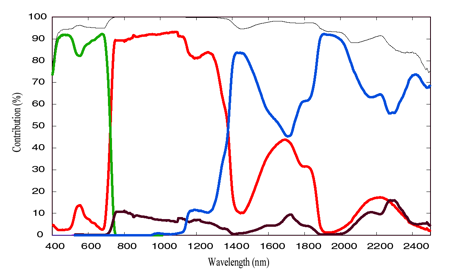
Figure 6. Contribution simulated by PROSPECT of chlorophyll concentration Cab (green), water content Cw (blue), dry matter content Cm (brown) and the structure parameter N (red) to the leaf transmittance. The black curve is the sum of the individual contributions.
The very last version of the model called PROSPECT-5 has separated the foliar pigments into the total chlorophylls and the total carotenoids (Feret et al., 2008). Finally, PROSPECT has been validated by inversion on reflectance and/or transmittance spectra of many leaves of various species from independent datasets (Newnham and Burt, 2001).
b) Compact Spherical Particle Models
None of these models were adapted to needle-shaped leaves that cannot be treated as discrete plane parallel layers. Dawson et al. (1998) adapted Melamed's theory of light interaction with suspended powders and designed the LIBERTY model (Leaf Incorporating Biochemistry Exhibiting Reflectance and Transmittance Yields) specifically to calculate the optical properties of both dried and fresh conifer (particularly pine) needles. Melamed (1963) considers discrete particles making a uniform compact layer and reflecting light diffusely according to the laws of geometrical optics. The calculation, which is developed for spherical particles that are assumed to be large compared with the wavelength, involves internal reflections within a particle and scattering of light between particles in the same relative plane (Figure 7).
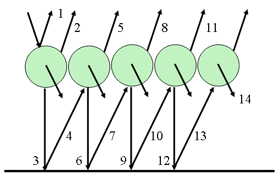
Application of the Lambert's cosine law over the whole volume of an idealized spherical particle yields the following expression for the radiation fraction reaching the particle surface after absorption in bulk:
(10)
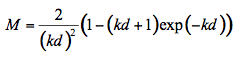
where k = k(λ) is the particle absorption coefficient at the wavelength λ, and d is the particle diameter. The statistical summations of all fluxes in Figure 7 gives the total transmittance fraction through a single particle layer T :
(11)
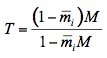
where
is the average internal reflection coefficient of the particle arising from reflection of photons at the vacuum-sphere interface. It is the Fresnel reflection coefficient integrated over all angles up to the critical angle 
c = sin-1(1/n), n, being the refractive index of the medium. The expression for the reflectance R, corrected by Mandelis et al. (1990), is then:
(12)
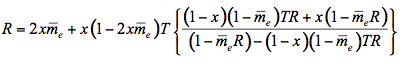
where x is the fraction of radiation scattered in the upward direction, expressed as a fraction of 4
steradians, and 
is the average external reflection coefficient of the particle. The reflectance is obtained by solving Equation 12, where the negative root only is retained for physically meaningful values (R 
1). Mandelis et al. (1990) propose the following expression for x:
(13)
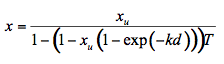
where xu represents the probability for diffuse scattering in the upward direction (0.1 < xu < 0.4). By treating the leaf as an aggregation of cells, with multiple radiation scattering between cells, output reflectance and transmittance spectra are a function of three structural parameters (cell diameter in µm, intercellular air space, leaf thickness) and the combined absorption coefficients of leaf biochemicals (chlorophyll concentration in mg m-2, water content in g m-2, lignin and cellulose content in g m-2, and nitrogen content in g m-2). To date, LIBERTY remains the only model used for this purpose.
c) N-flux Models
These models derive from the Kubelka-Munk (KM) theory that considers the leaf as a slab of absorbing (absorption coefficient k) and diffusing (scattering coefficient s) material (Kubelka and Munk, 1931). Infinite lateral extension and the absence of boundary reflections at the top and the bottom of the slab are first assumed in order to eliminate edge effects. The theory provides simple analytical formulae for the diffuse reflectance and transmittance in terms of k, s, and the thickness d of the medium. We consider hereafter the special case where k and s are independent of depth in the material but the theory can be extended to the case where they are both functions of depth with the same functional dependence (Mandelis and Grossman, 1992). The radiation field inside the slab consists of fluxes propagating in opposite directions. In the two-flux model, the intensities of the diffuse fluxes traveling in the forward I(x)and backward J(x)directions at depth x along the spatial axis and at any wavelength λ are coupled according to differential equations:
(14)
The incident flux is designed I0 = I(0) and considered unity. The reflectance R and transmittance T of the slab are given by the boundary conditions R = J(0) and T = I(d):
(15)
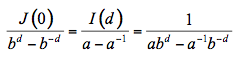
where a and b can be written as a function of k and s. The similarity between this expression and the solution of the generalized plate model (Equation 6) is notable. In the more rigorous four-flux model, radiation within the medium consists of two collimated and two diffuse fluxes propagating in opposite directions (Figure 8).
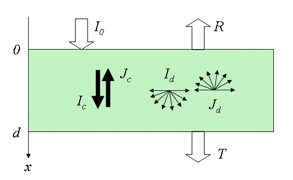
The flow of total fluxes can be written in differential form as:
(16)
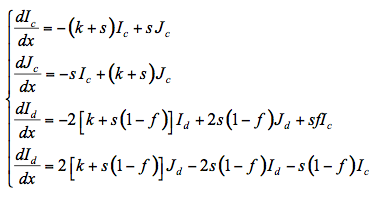
where Ic and Jc are the upward and downward collimated radiant fluxes, Id and Jd are the corresponding diffuse fluxes, and
is the asymmetry factor that describes the anisotropy of scattering. From the solutions of the previous system, we obtain collimated-collimated, collimated-diffuse and diffuse-diffuse components of reflectance and transmittance. According to Vargas and Niklasson (1997), the four-flux model compares well with numerical solutions of the equation of radiative transfer or with highly accurate Monte Carlo simulations. This is not surprising since the N-flux equations are a simplification of the radiative transfer theory. A two-flux model (Allen and Richardson, 1968; Cordon and Lagorio, 2007) and a four-flux model (Fukshansky et al., 1991; Martinez von Remisowsky et al., 1992; Richter and Fukshansky, 1996) have been successfully used in the forward mode to calculate the optical parameters of plant leaves. Yamada and Fujimura (1991) proposed a more sophisticated version in which the leaf was divided into four parallel layers: the upper cuticle, the palisade parenchyma, the spongy mesophyll, and the lower cuticle.
The KM theory is applied with different parameters in each layer, and solutions are coupled with suitable boundary conditions to provide the leaf reflectance and transmittance as a function of the scattering and absorption coefficients. The latter determined in the visible region was interpreted in terms of chlorophyll content and, by inversion, the four-layer model became a nondestructive method for the measurement of photosynthetic pigments. This approach was validated on leaves of both monocots - rice (Oryza sativa L.) and dragontree (Dracaena draco L.) - and dicots - hydrangea (Hydrangea L.) and chinquapin (Chrysolepis Hjelmquist). But these authors went further, reproducing the difference between reflectance from above and below, which is especially significant in dicotyledonous leaves. The leaf biochemistry has been introduced by Conel et al. (1993a, 1993b) who used a two-flux model to study the influence of water, protein, cellulose, lignin, and starch on leaf middle infrared reflectance. Unfortunately they did not validate it. Finally, a very simple model, directly issued from the expression of the reflectance, was used to estimate the chlorophyll content of wheat leaves (Andrieu et al., 1988). Finally, note that the parameter in the generalized plate model, which describes the leaf internal structure, plays a role similar to that of the scattering coefficients in the Kubelka-Munk model.
d) Radiative Transfer Equation
Propagation of light in plant leaves can, in principle, be described using fundamental electromagnetic theory. In this case the leaf is considered a random medium with a spatially varying permittivity εr and variations of the electric field would be described using Maxwell theory. However, such a treatment is troublesome because of the complexity of the problem and a lack of precise knowledge of εr. Instead the problem can be simplified by only considering the flow of energy through the medium. Although the radiative transfer equation was developed for three-dimensional media, the propagation of light in one direction will be considered hereafter. Let I(x,µ) be the intensity of monochromatic radiation at a position x in the interior of the leaf, traveling in a small volume element dx.dy, in the direction θ. We define µ = cosθ and µ' = cosθ' as the axial cosines of the angle of light propagation before and after scattering, respectively. On the one hand, radiation is lost by absorption and diffusion as it propagates into the medium:
(17)
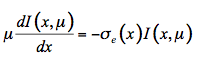
where
e(x) is the extinction coefficient of the medium defined as e(x) = k(x) + s(x). Equation 17 is nothing but the famous Beer's law. On the other hand, I(x) is intensified by two processes: coherent single scattering emerging from other directions and thermal emission of the medium, at the local thermodynamic equilibrium. The medium includes inhomogeneities in the form of small particles that scatter the radiation beam in all directions. The scattering is called coherent because the scattered radiation has the same wavelength as the incident radiation. The distribution of scattered radiation over all the directions is characterized by a phase function P(µ,µ') that is normalized to 1:
(18)
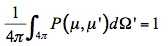
P(µ,µ') is the probability that the radiation falling in the direction µ of incidence will be scattered in the direction µ' of observation. As a consequence, the multiple scattering source function that corresponds to radiation falling on a volume element of the medium from all directions is equal to:
(19)
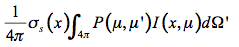
The thermal emission of this small volume element is expressed in terms of the Planck function for the intensity of radiation of an ideal blackbody M(T(x)):
(20)
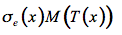
Then the source function J(x,µ) is the sum of these two processes:
(21)
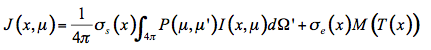
The radiative transfer equation that expresses the infinitesimal variation of flux dI in the infinitesimal slab at position x is an integro-differential equation:
(22)
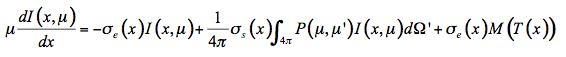
In the solar domain from 400 nm to 2500 nm, there is no thermal emission but intense scattering, so that Equation 22 simplifies:
(23)
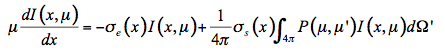
Solving Equation 23 with boundary conditions provides the diffuse reflectance and transmittance of the medium. Compared with canopy level, only few models directly use the radiative transfer equation at leaf level. The poor information we have on leaf internal structure and biochemical distribution leads to strong simplifications which make such an approach less efficient compared to more robust formulations. Because of the high water content of fresh leaves, Ma et al. (1990) modeled the leaf as a slab of water with an irregular surface containing randomly distributed spherical scatterers, the size distribution of which is Gaussian (Figure 9).
Radiation transfer theory and Kirchhoff rough surface scattering theory was applied to obtain the reflectance and transmittance of the leaf. The model was compared with bidirectional measurements made on corn (Zea mays L.), potato (Solanum tuberosum L.), and laurel (Prunus laurocerasus L.) leaves using a He-Ne laser operating at 632.8 nm, for normal illumination. Different configurations of polarization were tested with success on these leaves. In LEAFMOD (Leaf Experimental Absorptivity Feasibility MODel), the leaf is compared to a homogeneous mixture of biochemicals which scatter and absorb light (Ganapol et al., 1998). Absorption and scattering coefficients were calculated using reflectance and transmittance spectra simulated with PROSPECT, and reflectance spectra of stacks of Catalina cherry (Prunus lyonii) leaves measured at different water stages. Following the exploratory study of Hanrahan and Krueger (1993) and Franzke and Deussen (2003) for computer graphics applications, Wang et al. (2005) also used LEAFMOD to calculate subsurface scattering inside leaf tissues. In order to better represent the differentiated mesophyll of dicots, Berdnik and Mukhamed'yarov (2001) proposed a bilayer model made of two homogeneous layers differing in their concentrations of absorbing dyes and scattering particles. The first layer, i.e., the palisade parenchyma, was made of small spherical particles similar in volume to chloroplasts and having a refractive index of 1.42. The layer below, i.e., the spongy mesophyll, was made of large spherical particles full of air and then having a refractive index of 1. The refractive index of the surrounding medium in both layers was set to 1.36 equivalent with water. Finally, the size distribution of particles was described by a lognormal distribution. The novelty of this paper lies in the introduction of the Mie theory to calculate the scattering cross section of the particles. Experimental values of reflectance and transmittance obtained on Chinese holly (Ilex cornuta) leaves showed good agreement with the model both for illumination from above and below.
e) Stochastic Approach
Tucker and Garatt (1977) proposed an original model, LFMOD1, where the radiation transfer is simulated by a Markov chain, which is a stochastic process. As seen in Figure 10, they partitioned a black maple (Acer negundo L.) leaf into two independent tissues (palisade parenchyma and spongy mesophyll) and defined eight types of photon states (incident solar radiation, specularly reflected radiation, diffuse reflected radiation, diffuse transmitted radiation, absorbed and scattered radiation in each tissue). The random variable photon state can only take discrete values, like "absorbed in the palisade parenchyma" or "scattered in the spongy mesophyll". The system is then totally described by ten compartments connected by arrows that correspond to single-step transition probabilities from one photon state to another state between two compartments:
(24)
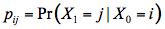
Figure 10. Representation of a typical dicotyledon leaf in LFMOD1. The boxes constitute the different photon states. The black ones are absorbing, the white ones are the non-absorbing, and the grey ones are the illumination states. The arrows show possible transitions [From Tucker and Garrett (1977), Applied Optics. Copyright © 1977 with permission from The Optical Society of America.]
The transition probabilities pij are most conveniently represented in a square array P of dimension 10 x 10, called transition matrix in which each row sums to one. They are set on the basis of the optical properties of the leaf material. The probabilities for the occurrence of these states are described by the elements of a column vector, pi, called state vector. Starting with an initial state vector p0 representing the incident radiation, the next state vector is obtained as p1 = Pp0, and after n steps we get:
(25)
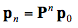
In the limit, the steady state that yields both the reflectance and transmittance is defined to be:
(26)
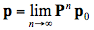
The SLOP (Stochastic model for Leaf Optical Properties) model (Lüdeker and Günther, 1990; Maier et al., 1999; Maier, 2000) is an improved version of the stochastic model, which differs in that the leaf is partitioned into four different tissues instead of two in the original work of Tucker and Garatt (1977). It implies introduction of additional photon states (Figure 11).
Figure 11. Representation of a typical dicotyledon leaf in SLOP. The boxes constitute the different photon states. The black ones the absorbing, the white ones the non-absorbing, and the grey ones the illumination states. The arrows show possible transitions [From Maier et al. (1999), Remote Sensing of Environment. Copyright © 1999 with permission from Elsevier.]
f) Ray Tracing Models
Among various approaches, only ray tracing techniques can account for the complexity of internal leaf structure as it appears in a photomicrograph. They require a detailed description of individual cells and their unique arrangement inside tissues. The optical constants of leaf materials (cell walls, cytoplasm, pigments, air cavities, etc.) also have to be defined. Using the laws of reflection, refraction, and absorption, it is then possible to simulate the propagation of individual photons incident on the leaf surface. Once a sufficient number of rays have been simulated, statistically-valid estimates of the radiation transfer in a leaf may be deduced. The technique has been applied with a number of variants. The first studies were performed at the cell level: Senn (1908), Haberlandt (1914), or recently Gabrys-Mizera (1976) and Bone et al. (1985) constructed geometrical models of light transmission through the cross-sections of plant cells of various shapes, in particular epidermal cells the shape of which might influence the path of the incident beams (Figure 12).
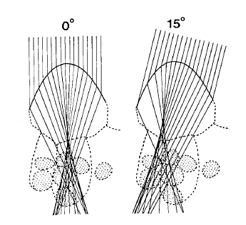
Figure 12. Ray diagram showing light refraction by leaf epidermal cells of Queen Anthurium (Anthurium warocqueanum) at zenith angles of 0o and 15o [From Bone et al. (1985), Applied Optics. Copyright © 1985 with permission from The Optical Society of America.]
Research efforts were also directed toward understanding the interaction of light with two-dimensional models of entire leaves. Willstätter and Stoll (1918) are often cited as the first authors who proposed a theory of leaf optics on the basis of critical reflection of light at cell wall-air interfaces (Figure 13).
Figure 13. Schematic drawing depicting the Willstätter and Stoll theory on the pathway of light through a dorsiventral leaf [From Sinclair et al. (1973), Agronomy Journal. Copyright © 1973 with permission from The American Society of Agronomy.]
Allen et al. (1973) built an albino maple (Acer negundo L.) leaf consisting of two media: cell walls characterized by their indices of refraction and intercellular space air. A 100 circular arcs model was used to test the specular and diffuse nature of the reflection. Simulations performed at 1 (m where absorption is very low led to an underestimation of the reflectance and an overestimation of the transmittance in the near-infrared plateau, which was demonstrated shortly afterwards by Kumar and Silva (1973) who found that the actual reflectance and transmittance of a soybean (Glycine max L.) leaf could be better reproduced by adding two more media into the model, cytoplasm and chloroplasts, thereby increasing the internal diffusion. Brakke and Smith (1987) incorporated more realistic representations of leaf anatomy by digitizing the geometrical structure of Allen's et al. (1973) maple leaf and Kumar and Silva's (1973) soybean leaf from electron micrographs. They also attempted to model the red pine (Pinus resinosa) needle described in Westman and price (1988) the year after. Such a needle-shaped leaf, which displays increased geometry compared to a lamina-shaped one, required about 600 arcs.
Whatever the approach, the absorption phenomena that characterize leaf optical properties outside the near-infrared plateau have been ignored. Moreover in all these models, leaves were always described as two-dimensional objects although the three-dimensional structure of these organs is very important to their physiological function. For this reason, Govaerts et al. (1996) used a three-dimensional ray tracing model, RAYTRAN (Govaerts and Verstraete, 1998), on a virtual 3D dorsiventral leaf represented in Figure 14, to characterize the light environment, including absorption, scattering and transmission, within and between cells: cells of variable size, cell wall thicknesses, chemistry and air spaces were modeled and implications for absorption profiles, light harvesting, and photosynthesis were successfully investigated (Ustin et al., 2001).
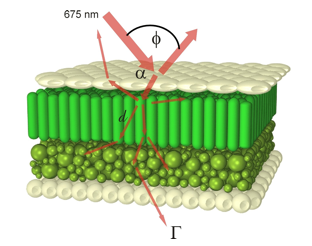
Figure 14. Perspective view of a virtual bifacial dicotyledon leaf illuminated at 675 nm. The cross-section of the target leaf is 300 mm x 300 mm x 170 mm (From Ustin et al. (2001), Plant Cell & Environment. Copyright © 2001 with permission from Blackwell Publishing.]
For applications in computer graphics, Baranoski and Rokne (1997, 1999) proposed a model called ABM (Algorithmic BDF Model) which takes into account biologically meaningful parameters that affect light scattering and absorption in leaves. Such an approach was quite new in this research community. Instead of modeling cells individually like in RAYTRAN, the propagation of light within the leaf tissues is simulated as a stochastic process where the transitions probabilities are driven by refraction at each interface (Fresnel reflection coefficients) and absorption in each tissue (Beer's law). These authors successfully simulated the reflectance and transmittance of a soybean (Glycine max) leaf but ABM seemed to be computationally expensive. They later introduced the FSM (Foliar Scattering Model) model, which gains efficiency over ABM by pre-computing reflectance and transmittance values and applying a simplified scattering model (Baranoski and Rokne, 2001). Both the ABM and FSM models are based on Monte Carlo ray tracing. These models have been recently adapted to better account for leaf complexity. Baranoski (2006) developed the ABM-U and ABM-B to investigate the interaction of light with unifacial and bifacial leaves that are characteristic of monocots and dicots, respectively. Finally Baranoski and Eng (2007) introduced the sieve effect that affects the optical properties of heterogeneous media.
Conclusion
Despite decades of research, much more work is required before we will accurately model leaf optical properties. Progress on the next generation of optical models requires improvements in understanding detailed cell and leaf anatomy for leaves having adaptations to different environmental conditions. Improvement in optical characterization (complex refractive index) of more biochemical compounds is needed to expand the range of biochemistry that can be detected. It is not currently possible to identify and quantify specific leaf pigments separately (e.g., chlorophylls a and b, anthocyanins, oxygen-free carotenes and xanthophylls). This information would significantly improve understanding of the biological controls on photosynthesis. Measurement and modeling of chlorophyll fluorescence could also provide critical information about photosynthetic functioning. When exposed to excess light, it is indeed a protective mechanism by which plant chloroplasts dissipate energy that exceed photosynthetic demands, thereby minimizing light-induced oxidative damage. It has been included in most leaf optics models but the latter are still in their infancy and therefore need to be improved and, above all, validated in terms of photosynthesis, plant physiological status, and photosynthetic functioning.
Leaf optical properties models have been integrated into canopy reflectance models which require reflectance and transmittance as input variables. For instance, the coupled PROSPECT + SAIL model, also called PROSAIL, is now widely used in the remote sensing community (Jacquemoud et al., 2008). LEAFMOD and LIBERTY were also linked to such models, but the distribution of these codes has remained limited compared to PROSAIL. Applications in computer graphics recently stimulated the rendering community to investigate this domain, because their main goal is to obtain realistic and real-time computer-based images (Baranoski and Rokne, 2004).
References
Allen W.A. and Richardson A.J. (1968), Interaction of light with a plant canopy, Journal of the Optical Society of America, 58(8):1023-1028.
Allen W.A., Gausman H.W., Richardson A.J. and Thomas J.R. (1969), Interaction of isotropic light with a compact plant leaf, Journal of the Optical Society of America, 59(10):1376-1379.
Allen W.A., Gausman H.W. and Richardson A.J. (1970), Mean effective optical constants of cotton leaves, Journal of the Optical Society of America, 60(4):542-547.
Allen W.A., Gausman H.W. and Richardson A.J. (1973), Willstatter-Stoll theory of leaf reflectance evaluated by ray tracing, Applied Optics, 12(10):2448-2453.
Andrieu B., Baret F., Schellberg J. and Rinderle U. (1988), Estimation de spectres de feuilles à partir de mesures dans les bandes spectrales larges, in Proc. 4th International Colloquium on Spectral Signatures of Objects in Remote Sensing, Aussois (France), 18-22 January 1988, ESA, Vol. SP-287, pp. 351-356.
Bacour C., Jacquemoud S., Tourbier Y., Dechambre M. and Frangi J.P. (2002), Design and analysis of numerical experiments to compare four canopy reflectance models, Remote Sensing of Environment, 79(1):72-83.
Baranoski G.V.B. and Rokne J.G. (1997), An algorithmic reflectance and transmittance model for plant tissue, in Proc. Conference of the European Association for Computer Graphics (Eurographics'97) (D. Fellner & L. Szirmay-Kalos, eds), Budapest (Hungary), Vol. 16(3), pp. 141-150.
Baranoski G.V.G. and Rokne J.G. (1999), A non-deterministic reconstruction approach for isotropic reflectances and transmittances, Journal of Visualization and Computer Animation, 10(4):225-231.
Baranoski G.V.G. and Rokne J.G. (2001), Efficiently simulating scattering of light by leaves, Visual Computer, 17(8):491-505.
Baranoski G.V.G and Rokne J.G. (2004), Light interaction with plants. A Computer Graphics Perspective, Horwood Publishing, 154 pp.
Baranoski G.V.G. (2006), Modeling the interaction of infrared radiation (750 to 2500 nm) with bifacial and unifacial plant leaves, Remote Sensing of Environment, 100(3):335-347.
Baranoski G.V.G. and Eng D. (2007), An investigation on sieve and detour effects affecting the interaction of collimated and diffuse infrared radiation (750 to 2500 nm) with plant leaves IEEE Transactions on Geoscience and Remote Sensing, 45 (8):2593-2599.
Baret F. and Fourty T. (1997), Estimation of leaf water content and specific leaf weight from reflectance and transmittance measurements, Agronomie, 17(9-10):455-464.
Benford F. (1923), Reflection and transmission by parallel plates, Journal of the Optical Society of America, 7(11):1017-1025.
Benford F. (1946), Radiation in diffuse medium, Journal of the Optical Society of America, 36(9):524-554.
Berdnik V.V. and Mukhamed'yarov R.D. (2001), Radiation transfer in plant leaves, Optics and Spectroscopy, 90(4):580-591 (cover-to-cover translation from Optika i Spektroskopiya, 90(4):652-663).
Bone R.A., Lee D.W. and Norman J.M. (1985), Epidermal cells functioning as lenses in leaves of tropical rain forest shade plants, Applied Optics, 24(10):1408-1414.
Brakke T.W. and Smith J.A. (1987), A ray tracing model for leaf bidirectional scattering studies, in Proc. 7th International Geoscience and Remote Sensing Symposium (IGARSS'87), Ann Arbor (MI), 18-21 May 1987, IEEE, pp. 643-648.
Breece H.T. and Holmes R.A. (1971), Bidirectional scattering characteristics of healthy green soybeans and corn leaves in vivo, Applied Optics, 10(1):119-127.
Carter G.A. (1991), Primary and secondary effects of water content on the spectral reflectance of leaves, American Journal of Botany, 78(7):916-924.
Ceccato P., Flasse S., Tarantola S., Jacquemoud S. and Grégoire J.M. (2001), Detecting vegetation water content using reflectance in the optical domain, Remote Sensing of Environment, 77:22-33.
Conel J.E., Bosch J.V.D. and Grove C.I. (1993a), Application of a two-stream radiative transfer model for leaf lignin and cellulose concentrations from spectral reflectance measurements. Part 1, in Proc. 4th Annual JPL Geoscience Workshop: AVIRIS (R.O. Green, ed), Washington (DC), 25-29 October 1993, JPL Publication, Vol. 93-26, pp. 39-43.
Conel J.E., Bosch J.V.D. and Grove C.I. (1993b), Application of a two-stream radiative transfer model for leaf lignin and cellulose concentrations from spectral reflectance measurements. Part 2, in Proc. 4th Annual JPL Geoscience Workshop: AVIRIS (R.O. Green, ed), Washington (DC), 25-29 October 1993, JPL Publication, Vol. 93-26, pp. 45-51.
Cordon G.B. and Lagorio M.G. (2007), Absorption and scattering coefficients: A biophysical-chemistry experiment using reflectance spectroscopy, Journal of Chemical Education, 84(7):1167-1170.
Dahm D.J. and Dahm K.D. (1999), Representative layer theory for diffuse reflectance, Applied Spectroscopy, 53(6):647-654.
Dawson T.P., Curran P.J. and Plummer S.E. (1998a), LIBERTY - Modeling the effects of leaf biochemical concentration on reflectance spectra, Remote Sensing of Environment, 65(1):50-60.
Feret J.B., François C., Asner G.P., Gitelson A.A., Martin R.E., Bidel L.P.R., Ustin S.L., le Maire G., Jacquemoud S. (2008), PROSPECT-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments, Remote Sensing of Environment, 112(6):3030-3043.
Fourty T., Baret F., Jacquemoud S., Schmuck G. and Verdebout J. (1996), Leaf optical properties with explicit description of its biochemical composition: direct and inverse problems, Remote Sensing of Environment, 56(2):104-117.
Fourty T. and Baret F. (1998), On spectral estimates of fresh leaf biochemistry, International Journal of Remote Sensing, 19(7):1283-1297.
Franzke O. and Deussen O. (2003), Accurate graphical representation of plant leaves, in Proc. Plant growth modelling and its applications (B.G. Hu & M. Jaeger, eds), Bejing (China), 13-16 October 2003, Springer-Verlag, pp. 16.
Fukshansky L., Fukshansky-Kazarinova N. and Martinez v. Remisowsky A. (1991), Estimation of optical parameters in a living tissue by solving the inverse problem of the multiflux radiative transfer, Applied Optics, 30(22):3145-3153.
Gabrys-Mizera H. (1976), Model considerations of the light conditions in noncylindrical plant cells, Photochemistry and photobiology, 24:453-461.
Ganapol B.D., Johnson L.F., Hammer P.D., Hlavka C.A. and Peterson D.L. (1998), LEAFMOD: a new within-leaf radiative transfer model, Remote Sensing of Environment, 63(2):182-193.
Govaerts Y., Jacquemoud S., Verstraete M.M. and Ustin S.L. (1996), Three-dimensional radiation transfer modeling in a dicotyledon leaf, Applied Optics, 35(33):6585-6598.
Govaerts Y. and Verstraete M.M. (1998), Raytran: a Monte Carlo ray-tracing model to compute light scattering in three-dimensional heterogeneous media, IEEE Transactions on Geoscience and Remote Sensing, 36(2):493-505.
Gronwall T.H. (1926), Reflection of radiation from a finite number of equally spaced parallel planes, Physical Review, 27:277-285.
Haberlandt G. (1914), Optical sense-organs, in Physiological Plant Anatomy (G. Haberlandt, ed), MacMillan and Co., London, pp. 613-631.
Hanrahan P. and Krueger W. (1993), Reflection from layered surfaces due to subsurface scattering, in Proc. Computer Graphics Proceedings (SIGGRAPH 93) (J.T. Kajiya, ed), Anaheim (CA), Vol. 27, pp. 165-174.
Jacquemoud S. and Baret F. (1990), PROSPECT: a model of leaf optical properties spectra, Remote Sensing of Environment, 34:75-91.
Jacquemoud S., Ustin S.L., Verdebout J., Schmuck G., Andreoli G. and Hosgood B. (1996), Estimating leaf biochemistry using the PROSPECT leaf optical properties model, Remote Sensing of Environment, 56(3):194-202.
Jacquemoud S., Bacour C., Poilvé H. and Frangi J.-P. (2000), Comparison of four radiative transfer models to simulate plant canopies reflectance - Direct and inverse mode, Remote Sensing of Environment, 74:471-481.
Jacquemoud S., Verhoef W., Baret F., Bacour C., Zarco-Tejada P.J., Asner G.P., Francois C. and Ustin S.L. (2008), PROSPECT + SAIL Models: a review of use for vegetation characterization, Remote Sensing of Environment, in press.
Kubelka P. and Munk F. (1931), Ein beitrag zur optik der farbanstriche, Zeitschrift fur Technische Physik, 12:593-601.
Kumar R. and Silva L. (1973), Light ray tracing through a leaf cross section, Applied Optics, 12(12):2950-2954.
Lüdeker W. and Günther K.P. (1990), Leaf reflectance: A stochastic model for analysing the blue shift, in Proc. Symposium on Global and Environmental Monitoring Techniques and Impacts, Victoria (BC), 17-21 September 1990, pp. 475-480.
Ma Q., Ishimaru A., Phu P. and Kuga Y. (1990), Transmission, reflection, and depolarization of an optical wave for a single leaf, IEEE Transactions on Geoscience and Remote Sensing, 28(5):865-872.
Maier S.W., Lüdeker W. and Günther K.P. (1999), SLOP: a revised version of the stochastic model for leaf optical properties, Remote Sensing of Environment, 68(3):273-280.
Maier S.W. (2000), Modeling the radiative transfer in leaves in the 300 nm to 2.5 µm wavelength region taking into consideration chlorophyll fluorescence - The leaf model SLOPE, PhD Thesis, Deutsches Fernerkundungstagsdatenzentrum, Technische Universität München, Oberpfaffenhofen (Germany), 110 pp.
Mandelis A., Boroumand F. and vanden Bergh H. (1990), Quantitative diffuse reflectance spectroscopy of large powders: the Melamed model revisited, Applied Optics, 29(19):2853-2860.
Mandelis A. and Grossmann J.P. (1992), Perturbation theoretical approach to the generalized Kubelka-Munk problem in nonhomogeneous optical media, Applied Spectroscopy, 46(5):737-745.
Martinez von Remisowsky A., McClendon J.H. and Fukshansky L. (1992), Estimation of the optical parameters and light gradients in leaves: multi-flux versus two-flux treatement, Photochemistry and photobiology, 55(6):857-865.
Melamed N.T. (1963), Optical properties of powders. Part I. Optical absorption coefficients and the absolute value of the diffuse reflectance. Part II. Properties of luminescent powders, Journal of Applied Physics, 34(3):560-570.
Newnham G.J. and Burt T. (2001), Validation of a leaf reflectance and transmittance model for three agricultural crop species, in Proc. International Geoscience and Remote Sensing Symposium (IGARSS'01), Sydney (Australia), IEEE, Vol. 7, pp. 2976 -2978.
Olf H.G. (1988), Stokes's pile of plates revisited, Journal of the Optical Society of America, 5(10):1620-1625.
Richter T. and Fukshansky L. (1996), Optics of a bifacial leaf: 1. A novel combined procedure for deriving the optical parameters, Photochemistry and photobiology, 63(4):507-516.
Senn G. (1908), Die Gestalts- und Lageveränderung der Pflanzen-Chromatophoren, W. Engelmann, Leipzig, 397 pp. Sinclair T.R., Schreiber M.M. and Hoffer R.M. (1973), Diffuse reflectance hypothesis for the pathway of solar radiation through leaves, Agronomy Journal, 65(2):276-283.
Stokes G.G. (1862), On the intensity of the light reflected from or transmitted through a pile of plates, Proceedings of the Royal Society of London. Series B, 11:545-556.
Tucker C.J. and Garratt M.W. (1977), Leaf optical system modeled as a stochastic process, Applied Optics, 16(3):635-642.
Tuckerman L.B. (1947), On the intensity of the light reflected from or transmitted through a pile of plates, Journal of the Optical Society of America, 37(10):818-825.
Ustin S.L., Jacquemoud S. and Govaerts Y. (2001), Simulation of photon transport in a three-dimensional leaf: implications for photosynthesis, Plant, Cell & Environment, 24:1095-1103.
Ustin S.L., Jacquemoud S., Zarco-Tejada P.J. and Asner G.P. (2004), Remote sensing of the environment: state of the science and new directions, in Manual of Remote Sensing. Volume 4: Remote Sensing for Natural Resource Management and Environmental Monitoring (S.L. Ustin, ed), John Wiley & Sons, pp. 679-729.
Vargas W.E. and Niklasson G.A. (1997), Applicability conditions of the kubelka-Munk theory, Applied Optics, 36(22):5580-5586.
Wang L., Wang W., Dorsey J., Yang X., Guo B. and Shum H.Y. (2005), Real-time rendering of plant leaves, in Proc. ACM SIGGRAPH 2005, Los Angeles (USA), 31 July - 4 August 2005, pp. 167-174.
Wessman C.A. (1990), Evaluation of canopy biochemistry, in Remote Sensing of Biosphere Functioning (R.J. Hobbs & H.A. Mooney, eds), Springer-Verlag, New York, pp. 135-156.
Westman W.E. and Price C.V. (1988), Spectral changes in conifers subjected to air pollution and water stress: experimental studies, IEEE Transactions on Geoscience and Remote Sensing, 26(1):11-21.
Willstatter R. and Stoll A. (1918), Untersuchungen uber die Assimilation der Kohlensaure, Verlag von Julius Springer, Berlin, 448 pp.
Yamada N. and Fujimura S. (1991), Nondestructive measurement of chlorophyll pigment content in plant leaves from three-color reflectance and transmittance, Applied Optics, 30(27):3964-3973.
11/20/08