Critical Transfer Distance Determination Between FRET Pairs
Antonie J.W.G. Visser1, Eugene S. Vysotski2, John Lee3
1Laboratory of Biochemistry and Microspectroscopy Centre, Wageningen University, 6703 HA Wageningen, The Netherlands
antoniejvisser@gmail.com
2Photobiology Laboratory, Institute of Biophysics, Russian Academy of Sciences, Siberian Branch, 660036 Krasnoyarsk, Russia
eugene_vysotski@ibp.ru
3Department of Biochemistry and Molecular Biology, University of Georgia, Athens, Georgia 30602, USA
jlee35uga@gmail.com
Objective
The use of fluorescence (or bioluminescence) spectra of the donor and absorption spectra of the acceptor as templates for an Excel (Microsoft) spreadsheet to calculate the critical transfer distance between any pair exhibiting Förster Resonance Energy Transfer (FRET). The method is illustrated with visible-fluorescent protein pairs, and with proteins involved in the bioluminescence of the jellyfish Clytia gregaria.
Introduction
FRET is a very powerful method for obtaining the distance (R) between proteins. FRET is currently one of the most applied methods used by scientists working at the interface of biology, chemistry, physics and optical engineering. It is based on the phenomenon that excited-state energy from a donor molecule is coupled non-radiatively to an acceptor molecule located nanometers away from the donor (Visser and Rolinski, 2010).
Figure 1 illustrates in the macroscopic world, a nice analogy of resonance energy coupling. When we strike a tuning fork with a mallet, sound waves are generated that can be transferred through space to another identical tuning fork. At the second tuning fork sound waves are produced at the same resonance frequency of the first tuning fork.
Figure 1. Resonance energy coupling between two tuning forks.
Jean Perrin and his son Francis Perrin postulated in the 1920s and 1930s that the mechanism of energy transfer is based on interacting, oscillating dipoles of donor and acceptor molecules. However, they obtained distances that were too long. Theodor Förster in the late 1940s succeeded in developing a quantitative theory of resonance energy transfer, which correctly predicted the distance dependence of the transfer rate constant. To achieve this theoretical model Förster followed several important steps:
i) Application of quantum mechanical theory of spectroscopic transitions.
ii) Expression of the transfer rate in terms of measurable quantities.
iii) Distance dependence of transfer rate is proportional to 1/R6.
iv) Concept of critical transfer distance, also called Förster radius, R0.
Since the transfer rate is proportional to the inverse 6th power of the distance R, the transfer rate is an extremely sensitive parameter for obtaining distances in the range of 1-10 nm (10-100 Å).
For a historical review of FRET that closes with Förster, see (Clegg, 2006). There is a vast amount of literature on FRET principles and applications, which is collated in (Lakowicz, 2006). The combination of FRET with optical microscopy, culminating in Fluorescence Lifetime Imaging Microscopy (FLIM) with many applications in the life sciences, has been reviewed recently by (Borst and Visser, 2010).
The kinetic scheme to explain FRET is presented in Figure 2 to emphasize that the interaction takes place between a donor molecule in the first excited singlet state, and an acceptor molecule in the ground state. It is also apparent from this scheme that the vibrational relaxation of the donor excited singlet state occurs prior to resonance energy transfer, implying that radiationless energy transfer is relatively slow, in agreement with the notion that there is a weak coupling between the transition dipole moments of both molecules.
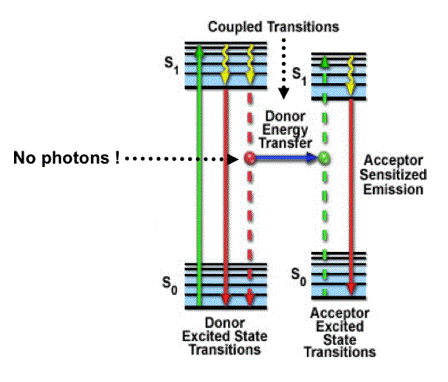
Figure 2. Jablonski diagram to explain the FRET process between a donor molecule and an acceptor molecule at nanometer separation. Absorption and emission transitions are represented by straight vertical arrows (green and red, respectively), while vibrational relaxation is indicated by wavy yellow arrows. The coupled transitions are drawn with dashed lines. The donor fluorophore can transfer excited state energy (blue arrow) directly to the acceptor without emitting a photon. The resulting sensitized fluorescence spectrum of the acceptor is identical to the one obtained after direct excitation. [Figure adapted from Figure 3 in the Optical Microscopy Primer]
Recapitulation of Relevant Equations
The FRET equations given in (Visser and Rolinski, 2010) have been duplicated here for ease of explanation. Förster derived the following equation for the rate constant of energy transfer kT from a donor molecule to an acceptor molecule a few nanometers away:
(1)
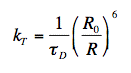
in which R is the distance between donor and acceptor molecules,
and
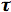D is the fluorescence lifetime of the donor in the absence of acceptor. The critical transfer distance R0 (in units of Å) can be calculated using the relevant spectroscopic properties of the participating molecules:
(2)
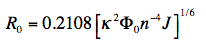
in which κ2 is the orientation factor, Φ0 the quantum yield of donor fluorescence (without acceptor), and n is the refractive index of the intervening medium. J (in units of M-1cm-1nm4) is the degree of spectral overlap between donor fluorescence spectrum (FD, its spectrum normalized so that the integral is equal to one), and acceptor absorption spectrum (scaled to its maximum molar extinction coefficient, εA, in units of M-1cm-1), given here in terms of wavelength λ (in units of nm):
(3)
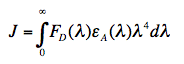
Förster also introduced the transfer efficiency E, which is only a function of actual (R) and critical (R0) distances:
(4)
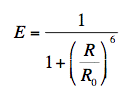
Judged from Equations 1 and 4, there are two ways of defining the critical transfer distance R0. According to Equation 1, R0 can be defined as that distance when kT is equal to 1/
D. According to Equation 4, R0 can be defined as that distance at which the excitation energy of the donor is transferred to the acceptor with probability 0.5.
Spreadsheet for Calculation of R0
In (Hink et al., 2003), corrected fluorescence excitation and emission spectra of several enhanced (E) variants of fluorescent proteins are collected, namely blue-fluorescent protein (EBFP), cyan-fluorescent protein (ECFP), green-fluorescent protein (EGFP), and yellow-fluorescent protein (EYFP), all derived from the original GFP from the jellyfish Aequorea victoria, and the red-fluorescent protein from the coral species Discosoma (DsRed). Note that corrected fluorescence excitation spectra are equivalent to absorption spectra (Visser and Rolinski, 2010). From these spectra the parameters required for quantization of resonance energy transfer (overlap integral, critical transfer distance) can be easily recovered following a computer program described in (Hink et al., 2003).
One of the authors (MAH) in (Hink et al., 2003) has incorporated the computer program into a Microsoft Excel spreadsheet. Here we demonstrate the Excel procedure with ECFP as donor, and EYFP as acceptor. This system has been described in (Visser and Rolinski, 2010) to illustrate the FRET process. You can download the spreadsheet file: calcR0_CFP-YFP2.xls [right click on a PC, or Option Click on a Mac]. The colored fields of its first worksheet, renamed FRET Table-1, are presented in Figure 3. To demonstrate the workings of the Excel FRET program, the digitized spectra for the CFP donor and the YFP acceptor are also included.
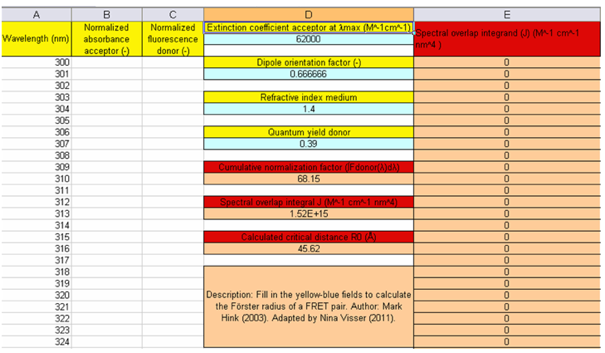
Figure 3. Colored fields of the first worksheet of the FRET spreadsheet (calcR0_CFP-YFP2.xls). The explanation is given in the text.
The first three columns (A, B, C) in Figure 3, labeled with headings in a yellow background, are for the wavelengths, the absorption spectrum of the acceptor, and the fluorescence spectrum of the donor (scroll down to 400-597 nm in the Excel file to see all the data). The maxima of both spectra have been normalized to one. The wavelengths are preset in the first column (A). The wavelength region is from 300 to 750 nm, with an increment of 1 nm. The absorption and fluorescence spectra are also recorded with 1 nm intervals.
The blue rows in column D (with headings in yellow) contain the input parameters. The first input parameter is the molar extinction coefficient of EYFP, which is used to scale the absorption spectrum that is normalized to unity at the maximum value. Its value is taken from literature, and amounts to 62000 M-1cm-1. The next input value is for the dipole orientation factor, κ2, which can adopt any value between 0 and 4 (see Visser and Rolinski, 2010). With the absence of structural information its value is often chosen as 2/3 or 0.666666, as in this example. This limiting situation is valid when the molecular dipoles are rapidly rotating at a speed much faster than the FRET rate. This is formally not true for slowly rotating fluorescent proteins.
A better approximation would be to take κ2 = 0.476, which is the value of the orientation factor for a rigid, randomized ensemble of donor and acceptor molecules (Steinberg, 1970). The next input parameter is for the refractive index (n) of the intervening medium. Its value for pure water is 1.333 (20 0C). Here n = 1.4 is chosen, which value can be considered as buffer salts dissolved in water. Finally, the quantum yield of the fluorescence of the donor (Φ0) must be given. Its value is taken from the literature, and amounts to 0.39.
The first output parameter (beige rows, column D) is the cumulative normalization factor (68.15), which is the integral value of the fluorescence spectrum of ECFP. The integral value of the spectral overlap is divided by this normalization factor to yield J = 1.52x1015 M-1cm-1nm4. The last output parameter is the calculated critical distance,
R0 = 45.62 Å.
The calcR0_CFP-YFP2.xls file contains a second worksheet, a graphical section with two charts (shown in Figure 4). Click on the "Charts" button at the bottom of the first worksheet. The first chart contains plots of the input parameters (columns A-C), the normalized absorption spectrum of EYFP, and the normalized fluorescence spectrum of ECFP. The second chart is the spectral overlap integrand calculated at the relevant wavelengths. The values are seen by scrolling down the fifth column, E, of the worksheet (heading has a red background). The summation of all values yields J = 1.52x1015 M-1cm-1nm4.
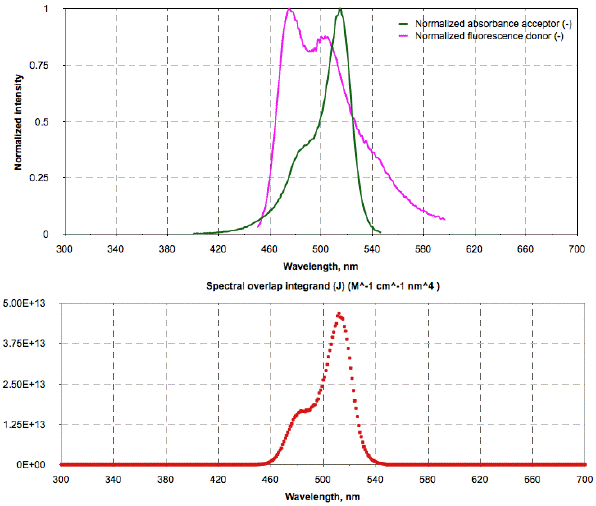
Figure 4. Top: Input spectra of donor (ECFP) and acceptor (EYFP) taken from the file calcR0_CFP-YFP2.xls. Bottom: Values of the spectral overlap calculated at each wavelength.
As an exercise to obtain insight into the dependence of the critical distance (R0) on the value of the orientation factor (κ2), make a list of the values of R0 as function of κ2 in the range 0.5 - 4.0 with increments of 0.5 (8 values in total). Graph these values to demonstrate the linearity of R0 as a function of (κ2)1/6. As another exercise, do the same to show the decrease of R0 as function of increasing values of the refractive index n. Make a plot of R0 versus n-2/3 for n values in the range 1.3-1.7, with increments of 0.05 to give 9 points on the graph. Show also the linearity.
FRET and BFRET in the Bioluminescent System of the Jellyfish Clytia gregaria
Green-Fluorescent Protein (GFP) is the origin of the green bioluminescence color exhibited by several marine hydrozoans and anthozoans. It is generally believed that GFP acts as an acceptor in a process of FRET, where the photoprotein bioluminescence excited state (S1) couples to the GFP's fluorophore ground state (S0) within a photoprotein-GFP complex. The function of GFP is that of an antenna protein. The term for this mechanism, Bioluminescence Resonance Energy Transfer (BRET), is now settled in the literature, but we would like to recommend "Bioluminescence-detected" FRET or BFRET. It is misleading to indicate "fluorescence" in FRET or "bioluminescence" in BRET, because photons are not involved in the coupling mechanism (see Figure 2). Furthermore, the "F" for Förster gives proper acknowledgement to the seminal contribution of Th. Förster to the theory (see Clegg, 2006).
Three papers dealing with the interaction of GFP with the photoprotein clytin from the jellyfish Clytia gregaria have been published recently (Markova et al., 2010; Titushin et al., 2010; Malikova et al., 2011). The addition of Ca2+ to purified photoproteins like clytin, produces a blue bioluminescence for clytin with a maximum at 475 nm. Clytin itself is not fluorescent, but the final product called Ca2+-discharged clytin, has a fluorescence maximum at 506 nm. Inclusion of GFP at µM concentrations shifts the bioluminescence spectrum to a 500 nm maximum to match the fluorescence of the GFP itself. It is proposed that FRET occurs between clytin and GFP in a protein-protein complex. For useful background information on bioluminescence, and an overview of the different bioluminescent systems, see Lee and Vysotski (2010).
The relevant spectra (with maxima normalized to 1) of the bioluminescence proteins from Clytia gregaria are collected in a Microsoft Excel document called Clytia_gregaria_spectra.xls. You can download the file: Clytia_gregaria_spectra.xls [right click on a PC, or Option Click on a Mac]. Note that this spreadsheet does not include the FRET program. It has only one worksheet, which contains the digitized spectral data in different columns for the purpose of the exercises. For the FRET calculation, the data have to be transferred, as will be described below. The data for the spectra are: column B, the fluorescence spectrum of the Ca2+-discharged clytin (410-598 nm); column E, the bioluminescence spectrum of clytin (370-558 nm); column H, the absorption spectrum of cgGFP (240-600 nm), and column K, the fluorescence spectrum of cgGFP (470-598 nm).
Let us focus on FRET between the Ca2+-discharged clytin (fluorescence spectrum), and the antenna protein cgGFP (absorption spectrum). Open the Microsoft Excel document calcR0_CFP-YFP2.xls, and save it with a new name, e.g., Ca-Clytin.xls. Delete the data in columns B and C. Go to the Clytia_gregaria_spectra.xls spreadsheet and copy column B, the fluorescence spectrum of the Ca2+-discharged clytin donor (410-598 nm), and paste it into column C of your new Ca-Clytin.xls spreadsheet, and paste column H, the absorption spectrum of the acceptor, cgGFP (300-600 nm), into column B of Ca-Clytin.xls. Pay attention that the data are aligned to the correct wavelengths. Input the appropriate parameters into the blue cells of column D. Markova et al. (2010) determined the extinction coefficient of the acceptor (ε=63030 M-1cm-1), and assumed the fluorescence quantum yield of the donor to be the same as the bioluminescence quantum yield of aequorin (0.175). By substituting these numbers in the input Table of Ca-Clytin.xls, together with n = 1.4 and κ2 = 0.476 (randomized static transition dipoles), the output parameters are J = 8.23x1014 M-1cm-1nm4 and R0 = 34.08 Å (Figure 5A).
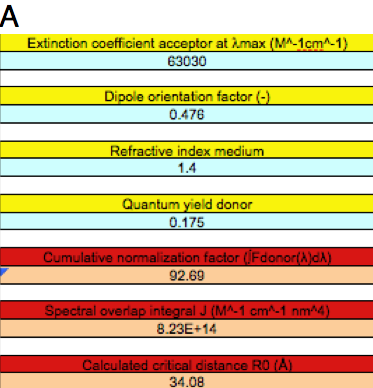
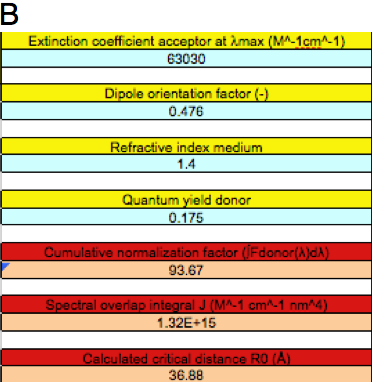
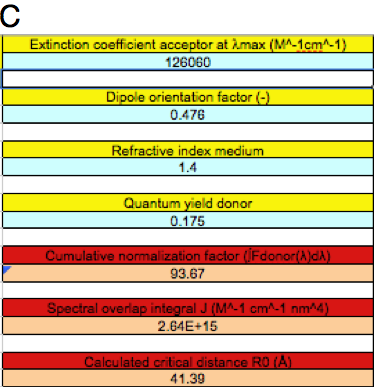
Figure 5. Different FRET situations as explained in the text.
A: FRET between excited Ca2+-discharged clytin and cgGFP.
B: BFRET between clytin bioluminescence and cgGFP.
C: as in B, but with twice the extinction coefficient of cgGFP.
Let us now focus on BFRET between the excited state corresponding to the bioluminescence of clytin (maximum 475 nm), and cgGFP as acceptor. This time rename and save the calcR0_CFP-YFP2.xls as BFRET.xls. Using similar procedures, as described in the previous paragraph, except copying the bioluminescence spectrum into column C, the output parameters are J = 1.32x1015 M-1cm-1nm4 and R0 = 36.88 Å (Figure 5B). The larger critical distance obtained as compared to excited Ca2+-discharged clytin as donor is completely accounted for by a larger overlap integral in the latter case, as the bioluminescence spectrum is more blue-shifted.
We have recently shown that cgGFP is an obligate dimer (Malikova et al. 2011). In other words, the whole protein acceptor contains two chromophores. The donor in the excited state "sees" two acceptor molecules, which makes the effective extinction coefficient twice as large (ε = 126060 M-1cm-1). When we substitute this value in the BFRET spreadsheet, the overlap integral is twice as large, and the critical distance increases (J = 2.64x1015 M-1cm-1nm4 and R0 = 41.39 Å, Figure 5C).
The quantum yield of donor fluorescence or bioluminescence (in the absence of resonance energy transfer) is also a controlling factor in the determination of the critical distance (see Equation 2). As an exercise to obtain insight into the dependence of the critical distance (R0) on the value of the quantum yield (Φ0), use the conditions shown in Figure 5C, and make a list of values of R0 as function of Φ0 in the range 0.1 - 1.0 with increments of 0.1 (10 values altogether). Make a plot of R0 versus (Φ0)1/6 to show the linearity.
The spatial structure of the clytin-cgGFP complex has been determined by computation based on the X-ray crystal structures of the separate proteins together with NMR constraints observed at high concentrations of mixtures of the two proteins (Titushin et al., 2010). In this computed structure, the donor and acceptor are separated by about 45 Å (R = 45 Å). Taking R0 = 41.4 Å (see above), then the efficiency of energy transfer E can be calculated from Equation 4 leading to E = 0.38 (or 38%; check this calculation). Of course, one would expect near 100% efficiency in agreement with the full color shift in bioluminescence observed by Markova et al. (2010). This can be achieved by optimization of the orientation factor and/or quantum yield of donor fluorescence. When the orientation factor increases from 0.476 to 4 (parallel transition dipoles in line) and the quantum yield approaches unity, this would increase the Förster radius from 41.4 to 78.91 Å (check this result by inputting these values into the BFRET.xls worksheet, FRET Table-1, using the conditions listed in Figure 5C), and the transfer efficiency from 0.38 to 0.97 (check this calculation using Equation 4). When these parameters are not optimized, it cannot be ruled out that the actual distance, R, between the chromophores might be shortened transiently during the bioluminescence reaction, which would also increase the efficiency close to E = 1.0.
Homo-FRET
cgGFP is an obligate dimer containing two identical chromophores. Therefore if one excites one GFP chromophore, part of the excited-state energy will be transferred to the other chromophore in the ground state, as demonstrated by Malikova et al. (2011). Radiationless energy transfer between identical molecules is called homo-FRET. As the 3-D structure of cgGFP is known (Titushin et al., 2010), we can directly determine the dipole orientation factor κ2 from the structure. It is found that κ2 =1.08 (Malikova et al., 2011). In addition, the actual center-to-center distance between the chromophores can be determined as R = 25 Å.
Again, use the Microsoft Excel document calcR0_CFP-YFP2.xls, copy this file and rename it, e.g., homoFRET.xls. Paste at the correct wavelengths in the relevant columns, the fluorescence spectrum of cgGFP (470-598 nm) and the absorption spectrum of cgGFP (300-600 nm). Markova et al. (2010) have determined the quantum yield of the fluorescence of cgGFP: Φ0 = 0.86. Note in Figure 6 that we use n = 1.6, because transfer is occurring between the chromophores in a dense environment of amino acids (Malikova et al., 2011). Note further that the extinction coefficient is for one chromophoric unit. It is found that J = 7.89x1014 M-1cm-1nm4 and R0 = 46.27 Å (Figure 6). By using Equation 4, we find for the FRET efficiency E = 0.97 (check this calculation). Malikova et al. (2011) found experimentally that R = 32 Å, leading to a FRET efficiency E = 0.90 (check this calculation).
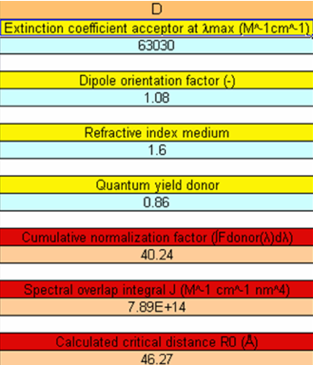
Figure 6. Homo-FRET parameters of two GFP chromophores. (For an explanation see text.)
Guide to Using the FRET Spreadsheet
It is important that the student obtains practice on how to use the FRET spreadsheet. Therefore, perform the described protocol to obtain the worksheets given in Figures 5A-C and 6. Keep the file calcR0_CFP-YFP2.xls as a "master" template, and make appropriate copies. Verify the obtained values for the spectral overlap integral, J, and Förster radius, R0. You can obtain graphs of the spectra in the graphical worksheet of Ca-Clytin.xls, BFRET.xls, or homoFRET.xls, by clicking on the "Charts" button at the bottom of the first worksheet.
Carry out the three exercises that are suggested in this module. Put the obtained data points pairwise in a Microsoft Excel spreadsheet. For instance, in the first exercise the orientation factor, κ2, increases from 0.5 to 4, with an increment of 0.5, and the corresponding R0 values must be calculated. Put R0 in the first column, and κ2 in the next column (8 data points per column). It is straightforward in Excel to calculate (κ2)1/6, and by using the "Insert Chart" option to make a graph of R0 versus (κ2)1/6. Perform this procedure for the other two exercises, and show the linear behavior of all three graphs. Carry out the four calculations of the transfer efficiency, E, by using Equation 4 for the clytin-cgGFP complex, and for the homo-FRET between the two chromophores in cgGFP.
The student may want to analyze his/her own experimental data with the supplied FRET spreadsheet. In calcR0_CFP-YFP2.xls the wavelengths are preset (300-750 nm) with 1 nm intervals, but feel free to change this column with wavelength intervals of 2 nm (or larger), or even variable wavelength spacings. This can be useful for checking the precision of the results, or if one wants to analyze a series of experimental data for quick estimates.
An easy experiment to perform with the master file calcR0_CFP-YFP2.xls (copy and rename as, e.g., test1.xls, test2.xls, etc.) is to delete the data points either from the absorption spectrum or from the fluorescence spectrum, and check whether the value of the spectral overlap integral (and thus the Förster radius) is affected. Take the fluorescence spectrum as an example, and delete data points such that the interval is 5 nm (save this as test1.xls), 10 nm (test2.xls), 15 nm (test3.xls), and 20 nm (test4.xls). You will notice that the value of the spectral overlap integral is the same for 1, 5 and 10 nm intervals, but becomes significantly unstable at higher intervals.
Question and Answer Section
More Questions? Contact the Authors.
Question:
How accurate are the values generated from the spread sheet?
Answer:
The excel spread sheet is a calculating program that finally produces a number: the critical distance, also called Förster distance or radius.
Assuming that the fluorescence spectrum of the donor and the absorption spectrum of the acceptor (both spectra normalized to 1 in the peak) are correctly introduced, then the only errors are those listed in column D of the spreadsheet.
Respectively:
1) the extinction coefficient at the maximum of the acceptor absorption spectrum (in the example 62000)
2) the dipole orientation factor (in the example 0.6666 corresponding to very rapidly rotating dipoles)
3) the refractive index of the solvent medium in which transfer takes place (in the example 1.4)
4) the quantum yield of donor fluorescence in absence of acceptor (in the example 0.39)
References
Borst JW and Visser AJW (2010) Topical review: Fluorescence lifetime imaging microscopy in life sciences, Meas. Sci. Technol. 21, 102002 (21 pp).
Clegg RM (2006) The history of FRET, in Reviews in Fluorescence, Vol. 3, (Geddes CD and Lakowicz JR, eds.) Springer, New York. Chap. 1, pp. 1-45.
Hink MA, Visser NV, Borst JW, van Hoek A and Visser AJW (2003) Practical use of corrected fluorescence excitation and emission spectra of fluorescent proteins in Förster Resonance Energy Transfer (FRET) studies. J. Fluoresc. 13, 185-188.
Lakowicz JR (2006) Principles of Fluorescence Spectroscopy, 3rd edn, Springer, New York, Chap. 13.
Lee J and Vysotski ES (2010) Structure and Spectra in Bioluminescence, on Photobiological Sciences Online (KC Smith, ed.). American Society for Photobiology, http://www.photobiology.info/.
Malikova NP, Visser NV, van Hoek A, Skakun VV, Vysotski ES, Lee J and Visser AJW (2011) Green-fluorescent protein from the bioluminescent jellyfish Clytia gregaria is an obligate dimer and does not form a stable complex with the Ca2+-discharged photoprotein clytin. Biochemistry 50: 4232-4241.
Markova SV, Burakova LP, Frank LA, Golz S, Korostileva KA and Vysotski ES (2010) Green-fluorescent protein from the bioluminescent jellyfish Clytia gregaria: cDNA cloning, expression, and characterization of novel recombinant protein. Photochem. Photobiol. Sci. 9, 757-765.
Steinberg IZ (1971) Long-range nonradiative transfer of electronic excitation energy in proteins and polypeptides. Annu. Rev. Biochem. 40, 83-114.
Titushin MS, Feng Y, Stepanyuk GA, Li Y, Markova SV, Golz S, Wang BC, Lee J, Wang J, Vysotski ES and Liu ZJ (2010) NMR-derived topology of a GFP-photoprotein energy transfer complex. J. Biol. Chem. 285, 40891-40900.
Visser AJW and Rolinski OJ (2010) Basic Photophysics, on Photobiological Sciences Online (KC Smith, ed.). American Society for Photobiology, http://www.photobiology.info/.
05/30/11